In the realm of product design, finding the optimal balance between form, function, and efficiency is crucial. Topology optimization has emerged as a powerful technique that revolutionizes the design process by utilizing computational algorithms to determine the most efficient distribution of material within a given design space. By exploring this innovative approach, designers can unlock new possibilities for creating lightweight, structurally sound, and high-performing products. In this article, we will delve into the concept of topology optimization, its benefits, and its applications across various industries.
Topology optimization is a computational design method that aims to optimize the distribution of material within a given design space to achieve specific performance objectives. By utilizing advanced algorithms and mathematical models, designers can explore countless design iterations, identifying the most efficient structural configurations while meeting the desired criteria. This process allows for the creation of designs that maximize strength-to-weight ratios, minimize material usage, and enhance overall performance.
Topology optimization enables designers to significantly reduce the weight of a product by removing excess material while maintaining structural integrity. This leads to improved energy efficiency, reduced manufacturing costs, and enhanced sustainability.
By exploring different design configurations, topology optimization can enhance product performance and functionality. The technique helps identify areas of stress concentration, enabling designers to reinforce critical regions and optimize load-bearing capacity, leading to superior performance and durability.
Topology optimization liberates designers from traditional constraints by allowing them to explore unconventional geometries. This fosters innovation and opens up new possibilities for unique, efficient, and aesthetically pleasing designs that were previously unattainable.
In the automotive and aerospace sectors, weight reduction plays a crucial role in improving fuel efficiency and reducing emissions. Topology optimization aids in designing lightweight and robust components, such as engine brackets, suspension systems, and aircraft structures, leading to enhanced performance and fuel economy.
In the medical field, topology optimization helps optimize the design of prosthetics, implants, and medical devices. By tailoring the internal structure and optimizing the load-bearing capacity, these products can provide better patient outcomes, comfort, and functionality.
Topology optimization finds application in architectural and civil engineering projects, enabling the creation of structurally efficient buildings and infrastructure. By optimizing material distribution, designers can reduce material usage, improve load-bearing capacity, and enhance structural stability.
While topology optimization offers numerous advantages, challenges remain, such as computational complexity, manufacturing constraints, and design validation. However, ongoing research and advancements in technology are addressing these challenges, making topology optimization more accessible and practical for a broader range of industries.

The first step in topology optimization is to define the design space, which represents the area where the optimization will take place. It is important to choose a design space that is sufficiently large to allow the solver to remove unnecessary material and explore different topologies effectively.
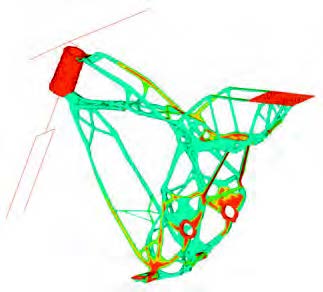
Geometric constraints are imposed to limit changes to specific regions of the design during the optimization process. These regions, known as frozen regions, remain unchanged while the solver extracts material from surrounding areas to find the optimal topology.

Determining the optimization objectives is crucial. In most topology optimizations, the goal is to maximize stiffness while minimizing the volume of the model. This is achieved by reducing strain energy within the model. However, it is also possible to optimize towards other objectives such as specific Eigenfrequencies or local displacements.
Assigning appropriate material properties is essential for accurate optimization. The properties define how the material behaves under different loading conditions, enabling the solver to simulate the structural response and optimize accordingly. Material properties include factors like density, Young’s modulus, and Poisson’s ratio.
Load and boundary conditions must be defined to simulate the real-world operating conditions of the design. These conditions include applied forces, fixed supports, and displacement constraints. By accurately defining these conditions, the optimization process can consider the structural response and find topologies that meet performance requirements.
The optimization process involves iterative iterations. The solver removes material from less critical areas and redistributes it to areas experiencing higher loads, aiming to achieve the defined optimization objectives. Iterations continue until a convergence criterion is met, indicating that the optimal topology has been reached.
After the optimization iterations, the results need to be analyzed and evaluated. This includes examining the achieved topology, evaluating its performance based on the defined objectives, and assessing factors such as stress distribution, displacement, and overall structural integrity.
Validation and refinement are important steps to ensure that the optimized topology meets the desired performance requirements. This can involve further analysis, simulation, or physical testing to validate the structural behavior and identify any potential issues. Based on the validation results, the design may be refined and optimized further if necessary.
Once the optimized topology is validated and refined, it can be finalized for implementation. This involves translating the optimized design into detailed engineering drawings or CAD models, considering manufacturing constraints, and preparing the design for production.
By following these steps, topology optimization enables engineers and designers to achieve optimized material distributions that improve structural performance, maximize stiffness, and minimize volume or other specific objectives, ultimately leading to more efficient and lightweight designs.
Topology optimization has revolutionized product design by leveraging computational algorithms to optimize material distribution within a given design space. With its ability to enhance efficiency, reduce weight, and improve performance, this technique holds immense potential across various industries. As technology continues to advance, topology optimization will play a crucial role in driving innovation, sustainability, and the creation of high-performing products that meet the demands of the future.
All medias & files courtesy of develop3d.com, unsplash.com
Posted By
kiran
Categories
Topology Optimization
Tags
Additive manufacturing, CAD, Topology optimization